サイン・コサインのわかりやすい説明　楽問（がくもん）のすすめ

直角三角形の辺の比率

おそらくこの説明がわからずに挫折した方も多いはず。私は、塾の講師や児童福祉の世界で高校生に勉強を教えたりする中で「どうやったら理解できるか」をひたすら考えてきました。

かつて、「答えがマイナスになる引き算」がどうしてもできない中学生の女の子がいて

教えるより自分がやる方が１００倍簡単

ということを思い知らされたことがあります。

今回は、sign（サイン） cosign（コサイン）の説明の仕方を思いつきました。すでに当たり前の説明方法かもしれません。

斜辺が１の直角三角形

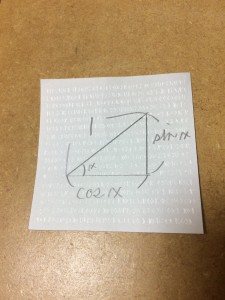
画像をみてください。斜辺が１で、左下の角度がＸ°の直角三角形です。そのときに

横の長さ=コサインＸ
縦の長さ=サインＸ

です。

なぜこれがいいのか？斜辺が１なので、計算が楽なのです。

斜辺が２だったら？

横の長さ=２コサインＸ
縦の長さ=２サインＸ

となります。

斜辺が１／２（２分の１）だったら？

横の長さ＝１／２コサインＸ
縦の長さ＝１／２サインＸ

となります。

これは斜辺が１だから簡単に計算が可能となるのです。

三角定規に使われている三角形を考えてみます。画像のＸの部分が４５°です。すると、

横の長さ＝コサイン４５°＝１／√2（ルート２分の１）
縦の長さ＝サイン４５°＝１／√2（ルート２分の１）

すべての辺に√2をかけると、

斜辺＝√2
横の長さ＝縦の長さ＝１

となり、１：１：√2の三角形と計算結果が一致します。