サインとコサインの意味を考えた　そうしたら話がルートにつながった

サイン、コサイン、タンジェント

知り合いの高校１年生が数学を勉強していて、「サインの２乗足すコサインの２乗は１だよ」と喜んでいた。



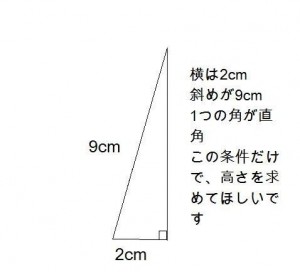
直角三角形の画像を探したらこれが見つかりました。数字や問題文は気にしなくてもいいです。

この画像の三角形で斜辺（画像では９センチになっている辺）が１センチだと考えてください。そして直角ではない方の角度をθ（シータ）で表すとすると、

signθ（サインシータ）は縦の辺の長さ

cosignθ（コサインシータ）は横の辺の長さ

になります。すると、「ピタゴラスの定理」※により、その女の子が言った

サインの２乗とコサインの２乗を足すと１になる

が成り立つことがわかります。


※「ピタゴラスの定理」

まさにこの画像の問題が「ピタゴラスの定理」です。求める縦の長さをx（エックス）とすると、

（２の２乗）＋（xの２乗）＝（９の２乗）

が成り立ちます。これを計算すると

（xの２乗）＝７７

なります。これは「２乗すると７７になる数」です。たとえばこれが「８１」なら「２乗にすると８１になる数」は「９」ですから簡単なのですが、「７７」だとそれを求めるのはかなり大変です。

ですから、その「２乗すると７７になる数」を「ルート７７」と「定義」したのです。



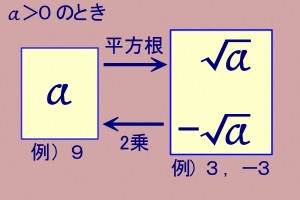
その高校生が「ルートの意味がわからない」と嘆いていましたが、ルートの計算の仕方にいろいろルールがありますから、そこで苦しんでいたのでしょう。